3x3 Identity Matrix

Finding a Circle Using. R allows creation of various different types of matrices with the use of arguments passed to the matrix function.

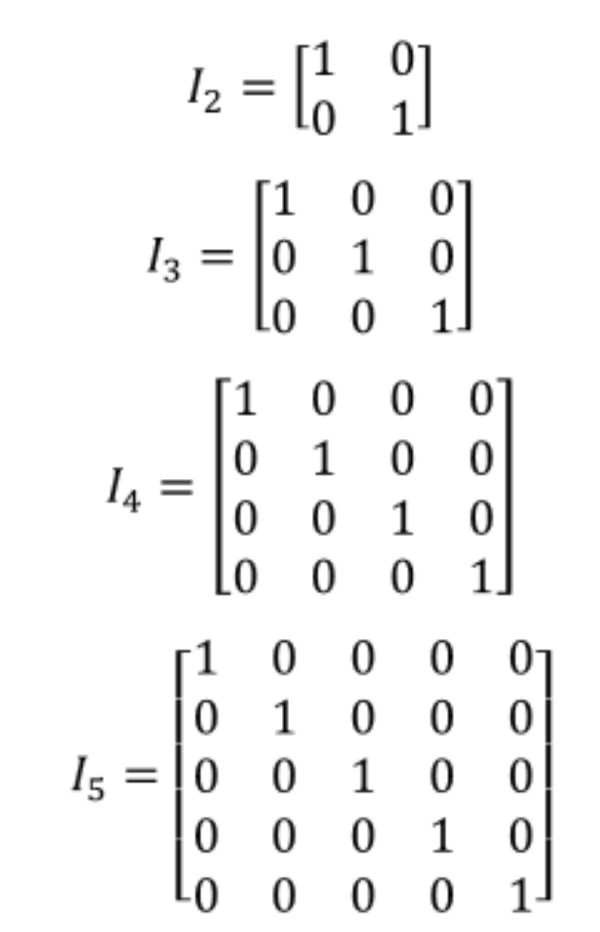
What Is An Identity Matrix Studypug

A camera is a mapping between.

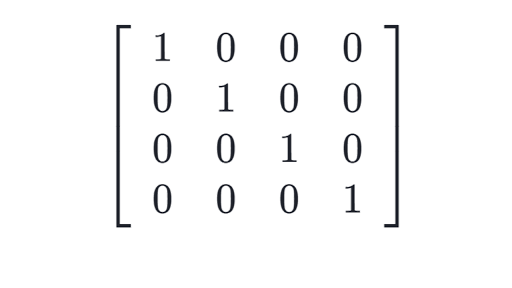
. The determinant of a triangular matrix is easy to find - it is simply the product of the diagonal elements. We need to multiply the numbers in each row of A with the numbers in each column of B and then add the products. Unlike general multiplication matrix multiplication is not commutative.

2x2 matrices are most commonly employed in describing basic geometric transformations in a. The eigenvalue problem is to determine the solution to the equation Av λv where A is an n-by-n matrix v is a column vector of length n and λ is a scalar. We are aware that a fraction is NOT defined if its denominator is 0.

Ie a square matrix A is singular if and only if det A 0. CNN Architectures Figure copyright Kaiming He 2016. Finding the Adjoint.

For any square matrix M of size m times m 2x2 3x3 4x4 etc eigenvalues are generally called lambda lambda and associated with an. Finding the Cofactor Matrix. Inverse of an nxn Matrix.

Here det A the determinant of A is in the denominator. Classmethod Identity size Create an identity matrix. Then we take this matrix and find the 3x3 determinant.

2D to 2D Transform last session 3D object 2D to 2D Transform last session 3D to 2D Transform today A camera is a mapping between the 3D world and a 2D image. Multiplying A x B and B x A will give different results. If A and A-1 are the inverses of each other then AA-1 A-1 A I.

To find the characteristic polynomial we first must subtract a matrix by an identity matrix multiplied by the scalar. A square matrix with all elements as zeros except for the main diagonal which has only ones is called an identity matrix. A new identity matrix.

Beware however that row-reducing to row-echelon form and obtaining a triangular matrix does not give you the eigenvalues as row-reduction changes. But what Im doing from all of these steps Im essentially multiplying both sides of this augmented matrix you could call it by a inverse. C d e a 1 2 3 b 4 5 6 c 7 8 9.

Finding the Pivot Positions and Pivot Columns. A square matrix is a matrix with the same number of rows and columns. 3x3 conv 512 3x3 conv 512 FC 4096 FC 1000 FC 4096 VGG16 VGG19 GoogLeNet.

Matrixk m n Parameters. These numbers are important because associated with their eigenvectors they make it possible to express the matrix in a simplified form which facilitates the calculations. 2x2 Matrix Multiplication Calculator is an online tool programmed to perform multiplication operation between the two matrices A and B.

The inverse of 3x3 matrix is used to solve a system of 3x3 equations in 3 variables. Size int The size of the identity matrix to construct 2 4. A matrix A is invertible inverse of A exists only when det A 0.

Important Notes on Inverse of 3x3 Matrix. The corresponding values of v that satisfy the. So I multiplied this by a inverse to get to the identity matrix.

But of course if I multiplied the inverse matrix times the identity matrix Ill get the inverse matrix. When writing a function taking Eigen objects as argument if you want your function to take as argument any matrix vector or expression just let it take a MatrixBase argument. The values of λ that satisfy the equation are the eigenvalues.

Input Softmax 3x3 conv 64 7x7 conv 64 2 FC 1000 Pool 3x3 conv 64 3x3 conv 64 3x3 conv 64 3x3 conv 64 3x3 conv 64 3x3. VDW eigA also returns full matrix W whose columns are the corresponding left eigenvectors so that WA DW. X PX camera matrix 3D world point 2D image point What do you think the dimensions are.

The inverse of a 3x3 identity matrix is itself. The eigenvalues are immediately found and finding eigenvectors for these matrices then becomes much easier. We would then set this entire thing equal to 0 to solve for the eigenvalue.

In linear algebra an n-by-n square matrix A is called invertible also nonsingular or nondegenerate if there exists an n-by-n square matrix B such that where I n denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplicationIf this is the case then the matrix B is uniquely determined by A and is called the multiplicative inverse of A. Camera Matrix 16-385 Computer Vision Kris Kitani Carnegie Mellon University. Inverse of a 2x2 Matrix.

Matrix where all rows and columns are filled by a single constant k. As an example here is a function printFirstRow which given a matrix vector or. A singular matrix is a square matrix if its determinant is 0.

To create such a matrix the syntax is given below. Finding Reduced Row Echelon Form. Hence A-1 is NOT defined when det A 0.

Eigenvalues are numbers that characterize a matrix. If a matrix consists only one column is called a column matrix. But anyway I dont want to.

Finding the Determinant of Large Matrices. We can only multiply two matrices if the number of rows in matrix A is the same as the number of columns in matrix B. Then we need to compile a dot product.

We know that the inverse of a matrix A is found using the formula A-1 adj A det A. The 3x3 matrix. You can specify typename as gpuArrayIf you specify typename as gpuArray the default underlying type of the array is double.

Noting that any identity matrix is a rotation matrix and that matrix multiplication is associative we may summarize all these properties by saying that the n n rotation matrices form a group which for n 2 is non-abelian called a special orthogonal group and denoted by SOn SOnR SO n or SO n R the group of n n rotation matrices is isomorphic to the group of rotations in. A matrix which contains only zeros as elements is called a zero matrix. To create a GPU array with underlying type datatype specify the underlying type as an additional argument before typenameFor example I eye3datatypegpuArray creates a 3-by-3 GPU identity matrix with underlying type datatype.

Finding the Determinant of a 3x3 Matrix. Classmethod LocRotScale location rotation scale Create a matrix combining translation rotation and scale acting as the inverse of the decompose. To find 3x3 determinants you would use the general method or the 3x3 matrix determinant trick known as the shortcut method.

Fei-Fei Li Justin Johnson Serena Yeung Lecture 10 - 6 May 4 2017 Last Time. Ie I-1 I.

How To Find The Determinant Of A 3x3 Matrix Youtube

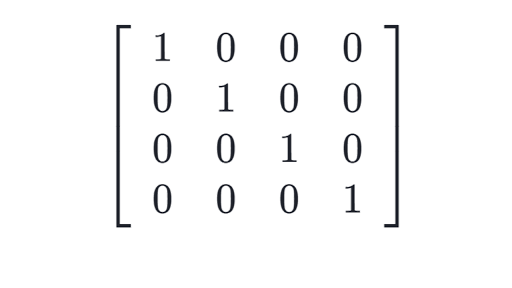
Identity Matrices

Identity Matrix Intro To Identity Matrices Article Khan Academy

Identity Matrix